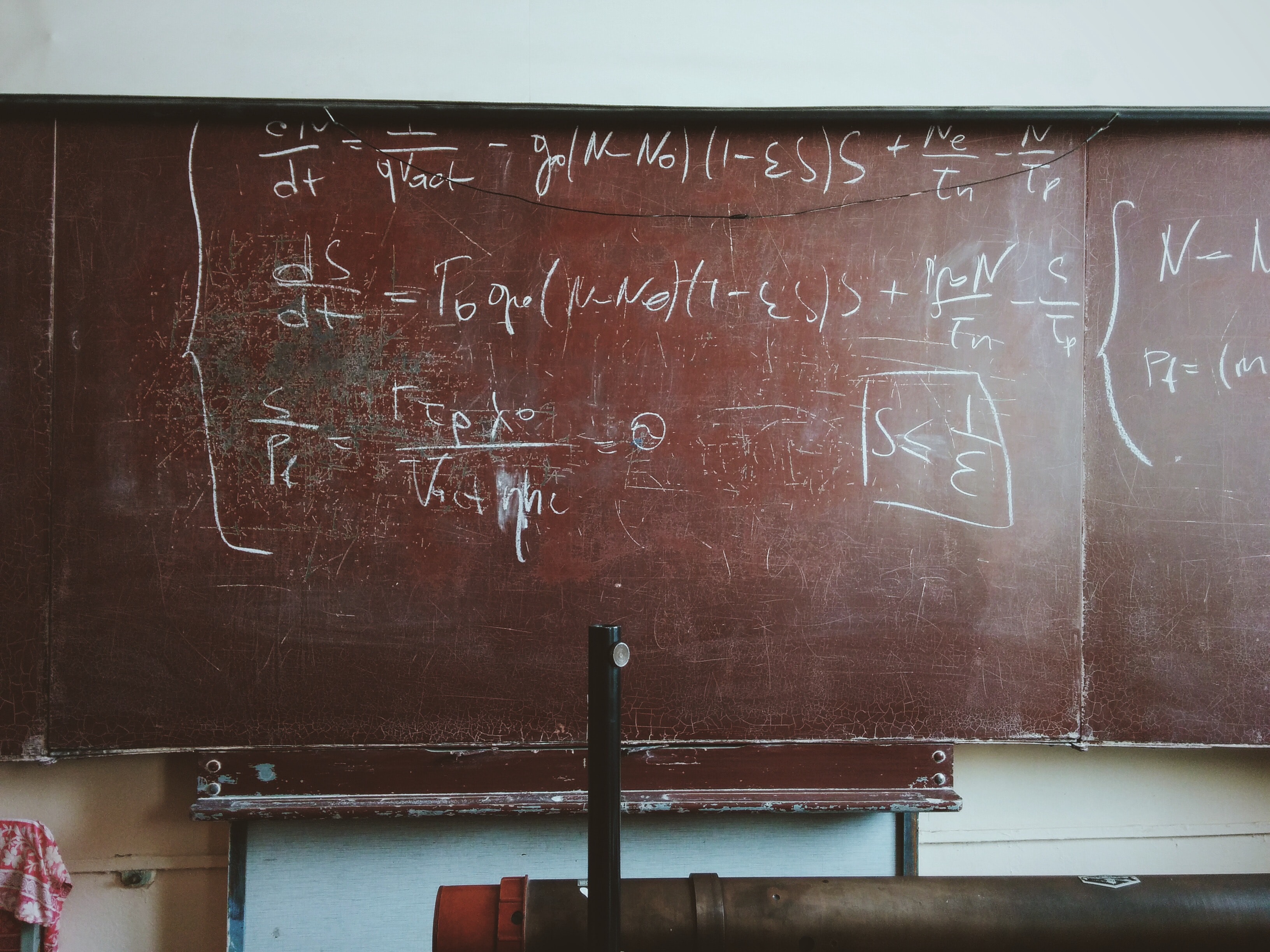
使用线性与其他非线性模型

2021-05-19

Contents

COVID-19 Case Study

昨日模型预估5月18日新增确诊病例数约为520-570例，实际新增确诊270例。误差为92.6-111% ，误差极大。误差原因为新增病例数较前一日减小，而指数模型假设为单调增加，因此造成较大误差。

由于疫情仍处于上升期，且数据点少，很难从本组数据中推断明日（5月19日）新增病例数会较前一日增加或减少。5月18日的降低可能是数据噪声，但也可能是实际在下降。

这时，使用更多其他数据作辅助判断的机器学习模型能够较好胜任预测。其原因在于机器学习模型是高维的、非线性的。高维的优势在于能够考虑多个变量对输出的影响。非线性的优势在于能有更真实地对现实情况进行建模。由于其复杂性，建立模型所需的知识储备和时间都较多，所以不在这里举例。

由于数据变动较大，今天我们除原先的指数模型，还考虑线性和其他非线性模型。

使用指数模型，我们有

$P(t) = Ae^{kt}$

除了原先提到过的局限性，还需要注意的是，指数模型只能够单调增加或单调减少。因此，在由增加转减少的时候不适用。这也是昨日模型误差大的原因。

今日，指数模型提示，若新增确诊病例数持续增加，则可以来到约380例，在300-400例的区间。

使用线性模型，我们有

$P(t) = kt+b$

与指数模型相同，线性模型只能够单调增加或单调减少。但是线性模型增加率比指数模型小得多。因此更加适用于疫情趋缓的情况。

今日，线性模型提示，若新增确诊病例数持续增加，则可以来到约360例，在300-400例的区间。 前几日的和平均的线性模型提示，新增确诊病例也可能到200例至400余例不等。

挑选适合的非线性模型，我们有

$P(t) = At^n e^{kt} + b$

作简单的分析，我们能够得知：

在 $t$ 较小时， $t^n$ 项主导该模型， $P(t)$ 持续依照 $t^n$ 的趋势增加（在此，一般有 $n \ge 1$ ）
- 当 $t \to 0$ 时， $P(t) \to b$ . 新增确诊数在初始状态
在 $t$ 较大时， $e^{kt}$ 项主导该模型， $P(t)$ 持续依照 $e^{kt}$ 的趋势减小（在此，一般有 $k < 0$ ）
- 当 $t \to \infty$ 时， $P(t) \to 0$ . 疫情结束，新增确诊数趋近于零
当 $t$ 达到最高点时， $P(t)$ 停止增加
- 求得导数，并将其设置为0，求得 $t$
- 可以估算到达高峰的时间
- 注意： $n \ge 1$ 且 $k < 0$ ，所以 $t>0$

$P'(t) = A(nt^{n-1} e^{kt} + k t^n e^{kt})$ $n+kt = 0$ $t = -\dfrac{n}{k}$

与先前模型不同的是，这里选择的非线性模型在最高点前单调增加，在最高点后或单调减小。该模型能更好地将疫情整体情况建模，但在面对更多复杂趋势时会无法适用。

例如，很多先前的数据点仅有单调增加或增加幅度不成比例地大，所以先前的模型都无法很好地拟合数据点。

由于减少的数据点的出现，该模型在今日能够更好地发挥其优势。

今日，非线性模型提示，若新增确诊病例数已经到达最高点并开始下降，则5月18日新增病例可以下降到约240例，在200-300例的区间。 值得注意的是，由于数据点较少，该假设仍需更多的数据的支持。

本文也发于微信公众号。