化学工程一维传热模拟
题目定义
求两端恒温的绝缘细棒的温度变化曲线。其中一端为高温 $T_{H} = 150 \mathrm{^\circ C}$,另一端低温 $T_L = 50 \mathrm{^\circ C}$。细棒初始温度为 $T_{i} = 10 \mathrm{^\circ C}$. 细棒有 $30 \ \mathrm{cm}$ 长。探讨不同材料的温度曲线。
解析解
我们有热传递方程
$$k\nabla^2 T + \dot{q} + \Phi = \rho C_V\dfrac{\partial T}{\partial t}$$
其中 $\nabla^2 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}$.
根据题目,我们有如下假设:
- 无热源/发热,为绝缘系统
- $\dot{q} = 0$
- 无流体或热运动
- $\Phi = 0$
- 细棒 $\implies$ 一维传热(在$y, z$方向没有传热)
- $\frac{\partial^2 T}{\partial y^2} = 0, \frac{\partial^2 T}{\partial z^2} = 0$
- 恒定热导率 $\implies k \not= f(x, y, z, t)$
- $k$ 可被化简
因此,我们可以简化热传递方程:
$$\begin{aligned} k\nabla^2 T + \dot{q} + \Phi &= \rho C_V\dfrac{\partial T}{\partial t} \\ k\nabla^2 T &= \rho C_V\dfrac{\partial T}{\partial t} \\ k\left(\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}\right) T &= \rho C_V\dfrac{\partial T}{\partial t} \\ k\frac{\partial^2T}{\partial x^2} &= \rho C_V\dfrac{\partial T}{\partial t} \end{aligned}$$
其中 $[k] = \mathrm{J m^{-1} s^{-1} K^{-1}}$ 为热导率,$[\rho] = \mathrm{kg/m^{3}}$ 为密度,$[C_V] = \mathrm{J kg^{-1} K^{-1}}$ 为比热容。
由热扩散系数的定义,我们有
$$k_{td} = \dfrac{k}{\rho C_V},$$
合并系数,可得
$$k_{td}\frac{\partial^2T}{\partial x^2} = \dfrac{\partial T}{\partial t}.$$
数值近似
我们可以通过中心有限差分法对二阶偏导数进行近似
$$\dfrac{\partial^2 T}{\partial x^2} \approx \dfrac{T_{i-1}^{\tau} - 2T_{i}^{\tau} + T_{i+1}^{\tau}}{\Delta x^2}$$
和正向有限差分法对一阶偏导数进行近似
$$\dfrac{\partial T}{\partial t} \approx \dfrac{T_{i}^{\tau} - T_{i}^{\tau+1}}{\Delta t},$$
其中 $i$ 为位置索引,$\tau$ 为时间索引。代入解析式,可得
$$k_{td}\dfrac{T_{i-1}^{\tau} - 2T_{i}^{\tau} + T_{i+1}^{\tau}}{\Delta x^2} = \dfrac{T_{i}^{\tau} - T_{i}^{\tau+1}}{\Delta t}.$$
整理该式,我们有
$$\begin{aligned} T_{i}^{\tau+1} &= T_{i}^{\tau}+\left(\frac{k_{t d}\Delta t}{\Delta x^{2}}\right)\left(T_{i-1}^{\tau}-2 T_{i}^{\tau}+T_{i+1}^{\tau}\right) \\ T_{i}^{\tau+1} &= T_{i}^{\tau}+\alpha\left(T_{i-1}^{\tau}-2 T_{i}^{\tau}+T_{i+1}^{\tau}\right) \end{aligned}$$
其中 $\alpha = \dfrac{k_{t d}\Delta t}{\Delta x^{2}}$.
有了这个表达式,我们就可以迭代并找到棒上各点在不同时间的温度。
材料属性
我们研究石墨、钛和金的温度曲线。石墨因其良好的导电性而被用于许多电和热学应用。钛因其低导电性和低密度而被用于航空航天应用。金的特点是其稳定性和良好的导电性。在这里,我们研究这些材料的细棒的温度曲线,以验证这些属性。
材料属性获取自 The Engineering ToolBox。
| 材料 | 密度 $\rho \ [\times 10^3 \mathrm{kg/m^{3}}]$ | 比热容 $C_V \ [\times 10^3 \mathrm{J kg^{-1} K^{-1}}]$ | 导热率 $k \ [\mathrm{J m^{-1} s^{-1} K^{-1}}]$ |
|---|---|---|---|
| 石墨 | 0.641 | 0.71 | 168 |
| 钛 | 4.5 | 0.47 | 20.4 |
| 金 | 19.29 | 0.13 | 312 |
结果
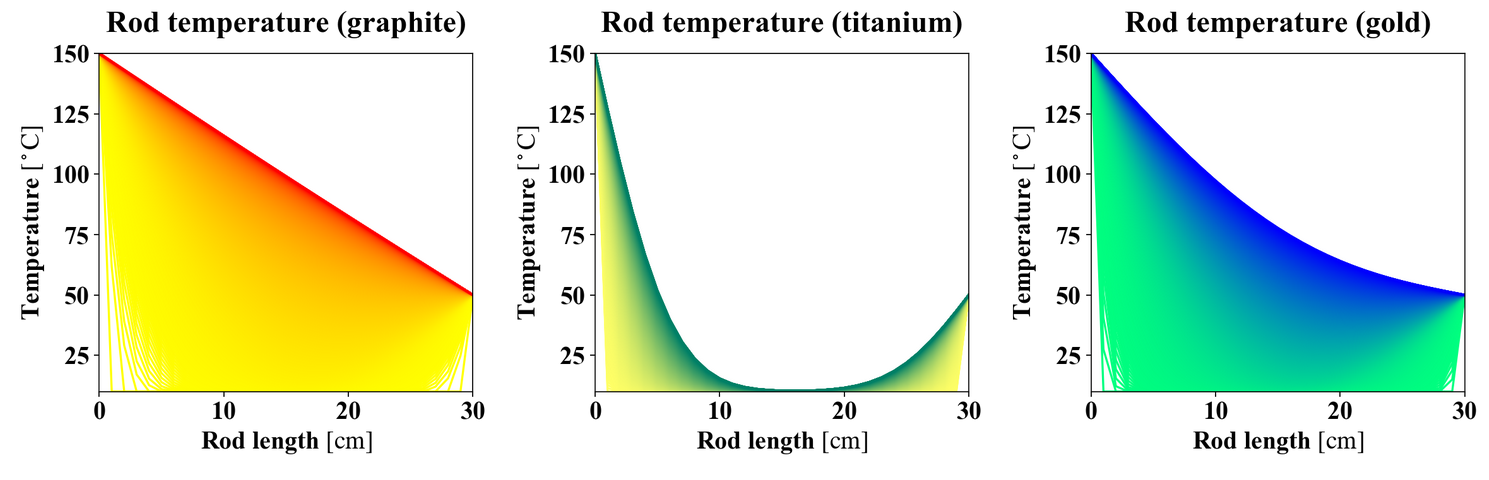
图一

如图一所示,较浅的颜色表示较早的时间,较深的颜色表示较晚的时间。热扩散系数高的石墨在 2 分钟的时间内达到平衡。热扩散系数相当的金也有较大的温度随时间变化,但它没有达到热平衡。热扩散系数低一个量级的钛显示出温度随时间的缓慢变化。只有与两端相邻的温度有明显的变化,而中心的温度在 2 分钟内没有变化。
由图一,我们可以得出,石墨和金是具有应用价值的良好热导体,而钛是导热慢,是空间应用的理想选择。
图二
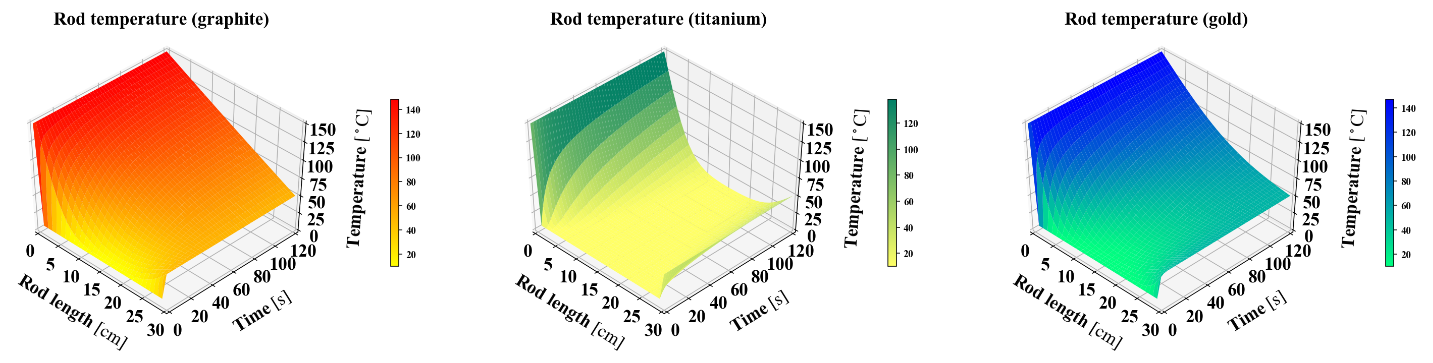
如图所示,浅色表示低温,深色表示高温。两端的温度恒定,而中间的温度随着时间的推移而增加。在最终时间,石墨的温度增加最多,而钛的温度增加最少。该结论与它们的热扩散系数相一致。
当互动模式打开时,三维图为较优选择,这样用户就可以旋转图表,看到三维的表面。当作为静态图像呈现时,三维图由于重叠和曲线等细节可能会丢失,因此并不理想。
可视化选择
假设这些图是用于静态的目的,如书籍、文章和演示,二维可视化更有效,因为三维图无法呈现二维静态图像中表面形状的细节。在二维图中,温度随时间变化的趋势是明显的,用户可以很容易地从最终的温度曲线上读出数值。尽管如此,二维绘图在表示时间轴上可能有限制。随着时间点数量的增加,线条聚集在一起,使人无法读出某个点在特定时间的温度。
假设这些图用于交互式目的,如交互式教程,图可以旋转以完全可视化表面形状(如使用 %matplotlib qt),三维可视化更有效,因为它给出了温度如何连续地随着细棒的位置和传导时间变化。然而,其使用情况是有限的。
附录
CHEME 375 Chemical Engineering Computing Skills Portfolio GitHub: https://github.com/tengjuilin/cheme-sci-computing
本文也发于微信公众号。